Research
My primary research interest is in mathematical epidemiology. Compartmental models of infectious disease provide a highly customizable framework which can be used to study disease dynamics. For example, the well-known Kermack-McKendrick (or SIR) model divides the population according to the stage of the disease and then tracks movement between the compartments using a system of nonlinear ordinary differential equations (ODEs).
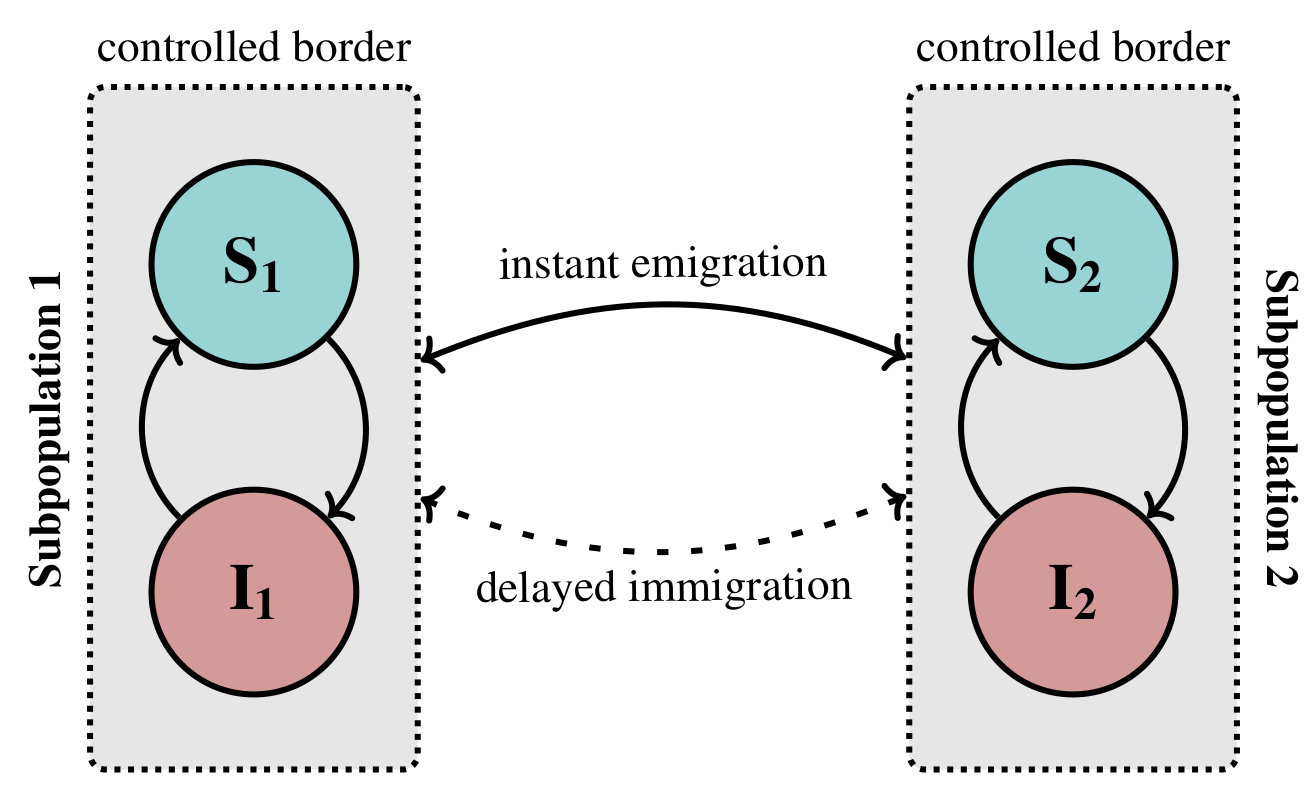
For my PhD dissertation (defended in September 2017), I worked on a project to model the spread of an infectious disease exhibiting susceptible-infectious-susceptible dynamics through a small metapopulation with delayed dispersal. Using that framework, I built a system of delay differential equations (DDEs) to model the scenario. While similar to ODEs in many ways, DDEs result in strikingly different behavior which may help to better account for certain disease dynamics; however, incorporating DDEs makes the system even more challenging to analyze.
At the Illinois Mathematics & Science Academy, I oversaw two high school students who developed their own framework for understanding COVID-19, and then built a deterministic model for transmission. Moving forward, I hope to build on this work and include more students in mathematical modeling. Even students with only a limited knowledge of calculus can begin to explore the world of mathematical epidemiology; and I would relish in the opportunity to help them start along that path.
In addition to my work in applied mathematics, I am also deeply interested in exploring how we understand and teach mathematics. I have conducted lots on informal research aimed at improving my own instruction; however I hope to continue building my expertise in this realm and eventually conduct more formal studies.